Odometry

Now that we know how to read the encoders on our mouse, we can use that to estimate the position and orientation of our mouse at any given time. This is a form of odometry.

Why is odometry important? Suppose we want our mouse to move forward by one maze cell. We could turn on both motors for a fixed amount of time, and hope the mouse moves exactly the distance we want it to. In practice, this doesn’t work due to friction, changing battery voltage, and many other factors. The difference between the desired movement and the actual movement is called error, and knowing the error is the first step towards correcting it.

Differential Drive Robot Odometry

Using the measurements from both wheels, we can compute the odometry for the entire mouse. Our mouse is a differential drive robot, which means that it has two drive wheels located side by side. Both wheels turning in the same direction causes forward (or backward) motion, and both wheels turning in opposite directions causes rotation.

When we describe the position and velocity of a robot, we are actually describing the position and velocity of a single point somewhere on the robot. For a differential drive robot like our mouse, this point is usually taken to be halfway between the wheels. Since a point can’t have a rotational velocity, the “point” is actually a coordinate frame. You can think of a coordinate frame as a set of coordinate axes that are “attached” to the mouse and move/rotate with it.

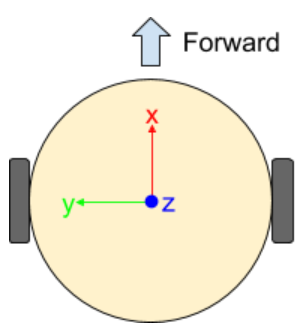
Consider the coordinate frame in the diagram above. When the mouse moves forward, it moves in the positive x direction. When the mouse rotates, it rotates around the z axis (which points upwards). The concept of coordinate frames is fundamental to robotics, but we won’t be able to cover it in much depth (try EECS C106A if you're interested in this type of stuff!). Fortunately, we only need to know some basics.

We are mostly interested in the forward velocity and rotational velocity of our mouse. Intuitively, the center of the mouse moves with a velocity that is the average of the wheel velocities. If both wheels move forward at the same speed, the center of the mouse moves forward with that speed. If the two wheels move in opposite directions at the same speed, the center of the mouse stays in place.

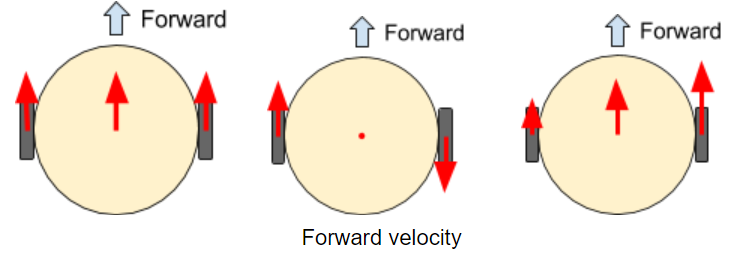
We can describe the forward velocity using the following formula where \(v_l\) is the left wheel velocity and \(v_r\) is the right wheel velocity:

$$v_f = (v_l + v_r)/2$$

We can also derive a formula for the rotational velocity of the mouse. Just as the forward velocity only depends on the sum (or average) of the two wheel velocities, the rotational velocity only depends on the difference of the two wheel velocities.

The speed of each wheel relative to the center of the mouse is half of the difference between their individual speeds. Rotational velocity is arc velocity divided by radius. We can describe the rotational velocity using the following formula where \(\omega\) is rotational velocity and \(d\) is the distance between the wheels (WHEELBASE_DIAMETER in the code):

$$\omega = (v_r - v_l)/d$$

Translate the formulas into Arduino code to fill in the TODOs below.

Checkoff #1

• How many millimeters does a wheel travel per encoder tick?
• The checkEncodersZeroVelocity() function sets wheel velocities to zero if it hasn’t seen an encoder pulse in 100 milliseconds. Why do we need this? Will the interrupt callbacks (leftEncoderRisingEdge() or rightEncoderRisingEdge()) ever set a wheel velocity to 0?
• Demonstrate your working code using Serial Plotter.